提供一种不用倒三角形也不用单调队列的做法。
题意
给定一个等边三角形的数字阵,求所有边长为给定值的子三角形的最大值之和。
思路
看到这题,很容易想到用一个类似 ST 表的东西来做。对于每个点,我们维护以该点为三角形上顶点的子三角形的最大值。参考 ST 表的做法,我们只用维护边长为 $2$ 的次方的子三角形,然后用某种方法拼出查询所需要的三角形就可以了。
怎么拼呢?设查询的三角形边长为 $h$,也就是题目中输入的 $k$,那么显然我们需要用边长为 $2^{\log_2 k}$ 的三角形来拼它。首先需要下图中的三个:
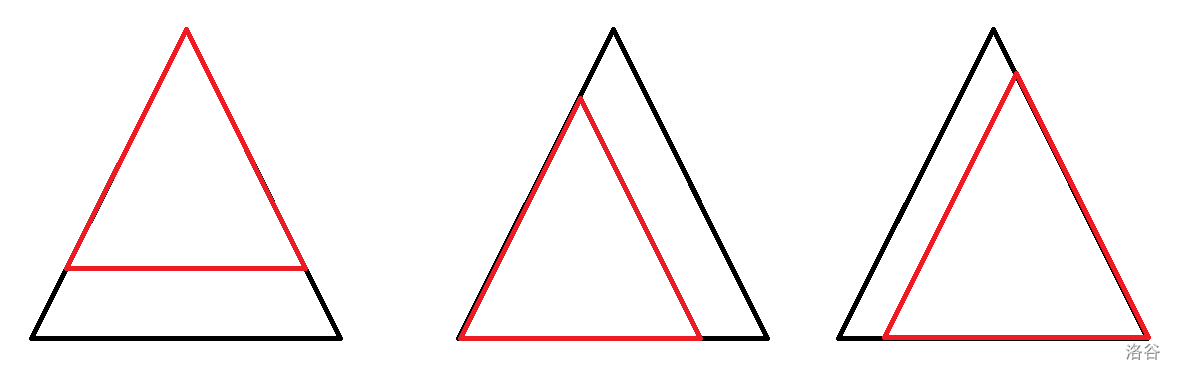
然后我们发现一个严重的问题:中间可能会有一个小三角形没有被覆盖到!
于是我们可以在底部正中间再放一个同样大小的三角形:
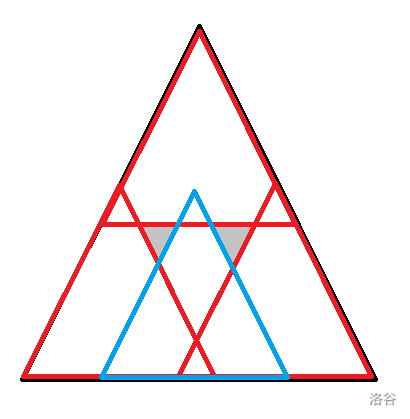
可是问题并没有完全解决,图中灰色的两块仍然没有被覆盖到啊……
于是我们发扬人类智慧:放一个不行,就放三个!
就有了下面这个:
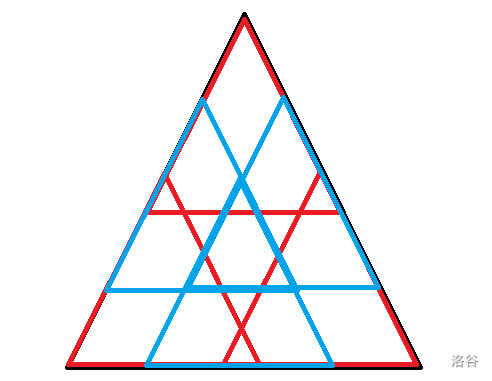
容易证明,这样一定可以把中间的部分覆盖完(考虑红色三角形边长恰好是大三角形边长一半的情况)。
实现细节
想到这些,我兴致勃勃的写完交了一发:MLE。然后发现被毒瘤出题人卡空间了。注意到这题的询问子三角形大小是固定的,因此我们的 ST 表可以滚动起来,保留 $\log_2 k$ 的值就可以了。另外位运算什么的细节也比较多,比较考验仔细程度。
丑陋的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include <bits/stdc++.h>
using namespace std;
int n,h,val[3005][3005],st[3005][3005][2],lg[3005],k;
long long ans;
int query(int x,int y){
int l=x+h-1,r=y+h-1;
int u=k&1;
int ans=max(st[x][y][u],max(st[l-(1<<k)+1][y][u],st[l-(1<<k)+1][r-(1<<k)+1][u]));
if(k<=1)return ans;
int cha=(h-(1<<k))>>1;
ans=max(max(ans,st[l-(1<<k)+1][y+cha][u]),max(st[x+cha][y][u],st[x+cha][y+cha][u]));
return ans;
}
signed main(){
freopen("star.in","r",stdin);
freopen("star.out","w",stdout);
cin>>n>>h;
k=log2(h);
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
scanf("%d",&val[i][j]);
st[i][j][0]=val[i][j];
}
}
for(int t=1;t<=k;t++){
int u=t&1,v=u^1;
for(int i=1;i+(1<<t)-1<=n;i++){
for(int j=1;j<=i;j++){
st[i][j][u]=max(max(st[i][j][v],st[i+(1<<t-1)][j][v]),st[i+(1<<t-1)][j+(1<<t-1)][v]);
if(t>1){
st[i][j][u]=max(max(st[i][j][u],st[i+(1<<t-1)][j+(1<<t-2)][v]),max(st[i+(1<<t-2)][j][v],st[i+(1<<t-2)][j+(1<<t-2)][v]));
}
}
}
}
for(int i=1;i<=n-h+1;i++){
for(int j=1;j<=i;j++){
ans+=query(i,j);
}
}
cout<<ans;
return 0;
}
|


