写在前面
这是一个有趣的问题。考场上死磕这个题 $2$ 小时,爆砍 $20$ 分,连第一档部分分都没拿到,只拿了爆搜的分。
考后看了信友队的录播讲评,又参考了魏老师的博客,总算把这个题写过了。这里分享一下。
题意
自己看吧,阅读 NOIP 原题题面有助于提高阅读理解能力。
思路
首先发现 $k=2n-2$ 或 $k=2n-1$,就不难想到我们每个栈里面只放两个元素。
对于 $k=2n-2$ 的情况,一定能使得有一个栈是空栈。因此对于每一个已经在栈里面的元素,如果在栈顶就直接消掉,否则放在空栈里和栈底直接消掉。
对于 $k=2n-1$ 的情况就要复杂得多了。我们很有可能出现一种可怕的情况:前面 $n-1$ 个栈里面已经存放了 $2n-2$ 个元素,这时出现了第 $2n-1$ 个元素!这时怎么办呢?
显然,这个新元素要么占掉我们仅有的那一个空栈,要么堆在某个已经放了两个元素的栈上面。
这时我们注意到一个东西:如果这个元素堆在一个已经放了两个元素的栈(令栈顶为 $a$,栈底为 $b$)上面,然后这个元素后面又紧跟了栈底元素 $b$ 的话,我们会立刻把后面的 $b$,放在空栈里,然后消掉,最后的效果是当前元素所在的栈只有两个元素,而我们依旧有一个空栈。也就是说,我们保持了之前需要的性质。
可是如果当前元素后面跟着的不是栈底元素 $b$,而是栈顶元素 $a$,那这个 $a$ 不就消不掉了吗?
这引导我们根据出现在当前元素后面的第一个栈底元素 $b$ 之前的 $a$ 的个数的奇偶性进行分类讨论。若出现了偶数个 $a$,那就让这偶数个 $a$ 自己消掉,不需要利用栈顶那个 $a$。此时显然可以按照前面的思路,把当前元素放在加入这个栈。若出现了奇数个 $a$,则必须要把栈顶的那个 $a$ 消掉。此时我们不得不将当前元素放入空栈。
什么?把当前元素放入空栈?那要是需要消掉栈底元素怎么办呢?别担心,我们之前的 $a,b$ 所在的栈是有所讲究的。我们要考虑的栈一定是 $b$ 出现的最早的栈,即我们找到当前元素之后第一个出现在栈底的元素进行处理。这时我们注意到 $b$ 上面是没有东西的,因此我们可以直接把 $b$ 给消掉,从而又恢复到最早的那个状态。由于 $b$ 的选择,我们在空栈出现之前是不会需要消掉栈底元素的,也就不需要空栈了。
放张图便于理解:
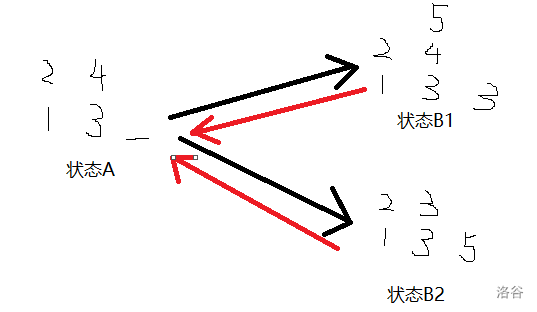
在这个图中,我们假设 $5$ 后面第一个出现的栈底元素是 $3$,这时我们根据出现在 $3$ 之前的 $4$ 的个数的奇偶性分类讨论。如果有偶数个,我们一定能到达状态 $B_1$,然后又返回状态 $A$;如果有奇数个,我们一定能到达状态 $B_2$,然后又返回状态 $A$。
还有一种情况,就是当前元素后面出现栈底元素之前又出现了一个当前元素。那我们可以直接把当前元素甩进空栈,与上面同理,是可以在需要空栈之前把当前元素消掉的。
通过这种方法,我们对每个出现在奇数位的元素都匹配了它的下一个出现在偶数位的元素,因此我们一定能找到一个解完成构造。
代码实现
要模拟上述过程并不难,就是细节比较多。魏老师说实现的精细可以做到 $O(n+m)$,我实现的不精细,因此是 $O(m\log n)$ 的复杂度。我用了一个 set 存储可以放元素的栈,用类似廊桥分配的做法维护;再开一些变量分别记录留空的栈,当前的状态 $A/B$。放一下核心部分的代码,变量名清奇不喜勿喷~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| n=read(),m=read(),k=read(),top=0,empty_stack=n;
for(int i=1;i<=m;i++)num[i]=read();
int now=0,yes=0,full=0;
set<int> st;
for(int i=1;i<n;i++)st.insert(i);
for(int i=1;i<=m;i++){
if(now&&num[i]==full){
ans[++top][0]=1,ans[top][1]=empty_stack;
continue;
}
if(now&&num[i]==yes){
ans[++top][0]=1,ans[top][1]=empty_stack;
ans[++top][0]=2,ans[top][1]=now,ans[top][2]=empty_stack;
now=0,yes=0,full=0;
continue;
}
if(bel[num[i]]){
if(up[bel[num[i]]]==num[i]){
ans[++top][0]=1,ans[top][1]=bel[num[i]];
if(sz[bel[num[i]]]==1){
up[bel[num[i]]]=dow[bel[num[i]]]=0;
}
else {
up[bel[num[i]]]=dow[bel[num[i]]];
if(bel[num[i]]!=empty_stack)st.insert(bel[num[i]]);
}
sz[bel[num[i]]]--,bel[num[i]]=0;
}
else{
ans[++top][0]=1,ans[top][1]=empty_stack;
ans[++top][0]=2,ans[top][1]=bel[num[i]],ans[top][2]=empty_stack;
if(sz[bel[num[i]]]==1){
up[bel[num[i]]]=dow[bel[num[i]]]=0;
}
else dow[bel[num[i]]]=up[bel[num[i]]],st.insert(bel[num[i]]);
sz[bel[num[i]]]--,bel[num[i]]=0;
}
continue;
}
if(!st.empty()){
int u=*st.begin();
ans[++top][0]=1,ans[top][1]=u,bel[num[i]]=u;
if(sz[u]){
up[u]=num[i],st.erase(st.begin());
}
else up[u]=dow[u]=num[i];
sz[u]++;
continue;
}
int u=i+1;
while(bel[num[u]]&&up[bel[num[u]]]==num[u])u++;
if(num[u]==num[i]){
ans[++top][0]=1,ans[top][1]=empty_stack;
bel[num[i]]=empty_stack;
up[empty_stack]=dow[empty_stack]=num[i],sz[empty_stack]=1;
continue;
}
int cnt=0;
for(int j=i;j<u;j++)if(num[j]==up[bel[num[u]]])cnt++;
if(cnt&1){
ans[++top][0]=1,ans[top][1]=empty_stack,st.insert(empty_stack);
bel[num[i]]=empty_stack;
up[empty_stack]=dow[empty_stack]=num[i],sz[empty_stack]=1;
empty_stack=bel[num[u]];
continue;
}
else{
now=bel[num[u]],ans[++top][0]=1,ans[top][1]=bel[num[u]],yes=num[u];
dow[bel[num[u]]]=full=up[bel[num[u]]],up[bel[num[u]]]=num[i];
bel[num[i]]=bel[num[u]],bel[num[u]]=0;
}
}
write(top),putchar('\n');
for(int i=1;i<=top;i++){
write(ans[i][0]),putchar(' ');
if(ans[i][0]==1)write(ans[i][1]),putchar('\n');
else write(ans[i][1]),putchar(' '),write(ans[i][2]),putchar('\n');
}
|
