AGC056A 题解
考试的时候做到这道题,很多小朋友好像都是坐板凳搜出来的捏~
老用户花了好久终于手玩出了一个构造方案,感觉还算比较简洁,分享给大家。
对于 $n\equiv 0 \pmod{3}$ 的情况
不难发现,我们有一种比较简单的构造方案,即每行循环移位 $3$ 格:
1 | ###...... |
这样就比较简单地解决了这种情况,相信大家都能想到。
对于 $n\equiv 1 \pmod{3}$ 的情况
我们试图基于上面的情况做一些调整。首先还是每行移位 $3$ 格:
1 | ###.... |
这时我们发现连通块个数不对呀?怎么办呢?
注意到,我们可以把这个图看做 $3$ 组:每一组刚好占满一整行。则上图中第一组的最后一行和第二组的第一行重叠了,多产生了一个连通块。这时我们想通过调整消去第一组的一个连通块,即上图中第三行的最后一个 #。
我们需要用到一个调整的操作:如果 $(x_1,y_1),(x_2,y_2)$ 都染了色,我们可以调整为给 $(x_1,y_2),(x_2,y_1)$ 染色。这个操作的对行列个数显然是没有影响的。我们可以拿他来改变连通块个数。
回到上面,我们考虑把第三行的最后一个 # 和第四行的最后一个 # 拿来调整,会发现连通块的个数刚好减少了!给下面最对称操作后得到的图是这样的:
1 | ###.... |
归纳一下:在循环移位后,我们给 $(n/3+1,n),(n/3\times2,n-2)$ 这两个位置和他们的对称位置分别做调整,就可以构造出解。
对于 $n\equiv 2 \pmod{3}$ 的情况
有了上面的经验,这一步就简单多了。大家可以自己手玩一下,这里给出归纳结论:在循环移位后,我们给 $(n/3+1,1),(n/3\times 2+1,n-3)$ 这两个位置和他们的对称位置分别做调整,就可以构造出解。
这样,我们就解决了这道题!是不是很简洁呢?当然还有其他的构造/坐板凳方法,大家可以私信 @赵悦岑 了解。
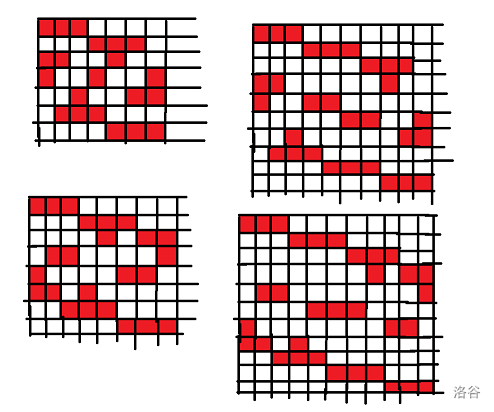
最后放一个 $n=7,8,10,11$ 的构造图希望能帮助到大家: